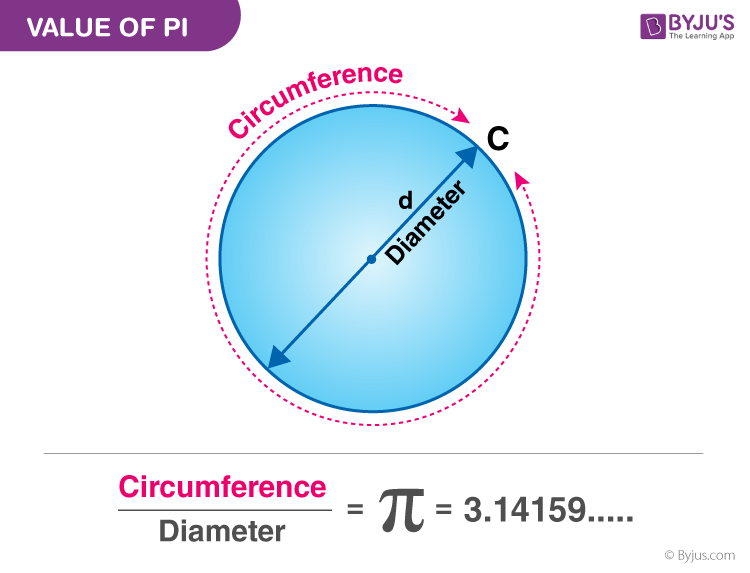
pi123: there exist constants that hold profound significance. Among them, pi, denoted as π, is a cornerstone, representing the ratio of a circle’s circumference to its diameter. However, the horizon of mathematical theory has expanded, giving birth to pi123, a groundbreaking concept that pushes the boundaries of traditional understanding.
Unraveling the Enigma: What is pi123?
Defining pi123
Pi123 is not just a single constant but an entire family of transcendental numbers, each with its unique properties and applications. Unlike pi, which is an irrational number, pi23 introduces a new level of complexity to mathematical theory.
The Genesis of pi123
The inception of pi123 can be traced back to the meticulous work of contemporary mathematicians who sought to delve deeper into the mysteries of transcendental numbers. Through rigorous exploration and innovative methodologies, they unearthed this new family of constants, revolutionizing the mathematical landscape.
The Significance of pi123 in Modern Mathematics
Applications in Geometry and Trigonometry
Pi123 extends its influence far beyond the realm of circles. It plays a pivotal role in advanced geometry and trigonometry, providing solutions to problems that were once deemed insurmountable.
Implications for Number Theory
Within number theory, pi123 serves as a catalyst for exploring the properties of transcendental numbers, shedding light on previously uncharted territory and prompting further inquiry.
Challenges in Understanding pi123
Navigating the Complexity
Due to its intricate nature, comprehending p123 requires a deep understanding of advanced mathematical concepts. This complexity poses a challenge even to seasoned mathematicians, prompting them to adapt and expand their cognitive frameworks.
Computational Limitations
Calculating pi123 to a high degree of precision demands immense computational power. This presents a practical obstacle for researchers aiming to utilize pi23 in real-world applications.
The Future of Mathematical Exploration with pi123
Potential for Technological Advancements
As researchers continue to unravel the mysteries of pi23, its applications in various technological fields are poised to be transformative. From cryptography to simulations, the impact of pi23 promises to be far-reaching.
Inspiring Future Generations
The discovery of pi23 serves as an inspiration for budding mathematicians, encouraging them to pursue their own inquiries and potentially uncover even more groundbreaking concepts in the future.
Conclusion
In the ever-evolving landscape of mathematics, pi123 stands as a testament to the boundless potential of human intellect. Its emergence opens up new vistas of exploration, inviting mathematicians to push the boundaries of what is known and embark on journeys of discovery.
Frequently Asked Questions
1. What distinguishes pi123 from the traditional constant pi (π)?
Pi123 represents an entire family of transcendental numbers, each possessing unique properties. Unlike pi, which is an irrational number, pi23 introduces a new level of complexity to mathematical theory.
2. How does pi123 impact practical applications in fields like technology and cryptography?
The discovery of pi123 holds immense potential for technological advancements. Its applications range from cryptography to simulations, promising to revolutionize various technological fields.
3. Are there any ongoing research efforts focused on further understanding pi123?
Yes, the mathematical community is actively engaged in ongoing research to deepen our understanding of pi123. This includes endeavors to calculate it with greater precision and explore its applications in diverse domains.
4. Can pi123 be expressed as a finite decimal or fraction?
No, like its predecessor pi (π), pi23 is a transcendental number, meaning it cannot be expressed as a finite decimal or fraction. Its decimal expansion is infinite and non-repeating.
5. How might the discovery of pi123 inspire future generations of mathematicians?
The emergence of pi23 serves as a source of inspiration for aspiring mathematicians, encouraging them to embark on their own journeys of inquiry and potentially uncover even more groundbreaking concepts in the future.
